Лекция 13.
6.2 Основные параметры кулачковых механизмов.
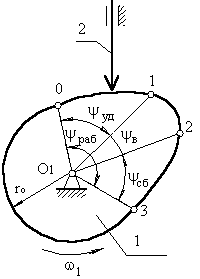
В процессе работы толкатель совершает в соответствии с
рисунком 3 движения:
1.
поступательно
вверх – в этом случае толкатель взаимодействует с участком 01;
2.
стоит
на месте (выстой) –
контакт с участком 12.
Здесь постоянный радиус кривизны.
3.
толкатель
опускается (сближение) – контакт с участком 23.
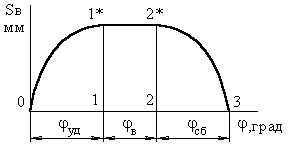
В первой фазе подъему толкателя (фаза удаления) на профиле
кулачка соответствует угол ψудал;
в фазе выстоя – ψвыс;
в фазе сближения – ψсб.ψудал + ψвыс + ψсб = ψраб – рабочий угол профиля кулачка.
Угол профиля кулачка можно показать только на кулачке.
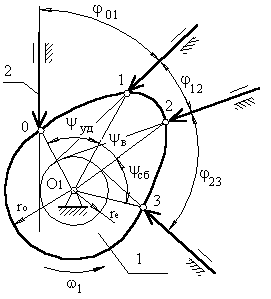
Угол поворота кулачка, соответствующий выше
указанным фазам перемещения толкателя, определяют, используя метод
обращения движения, в соответствии с которым всей системе, включая стойку,
мысленно сообщают движение с угловой скоростью (ω1).Тогда в обращенном движении кулачок становится неподвижным:
ω*1
= ω1 + (–ω1) = 0,
а ось толкателя вместе со стойкой будут перемещаться в
направлении (–ω1). И угол поворота кулачка,
соответствующий той или иной фазе движения, определяется по углу поворота оси
толкателя в обращенном движении на соответствующем участке. Ось толкателя в
обращенном движении в любом положении будет касаться окружности радиуса rе.
Поворот кулачка на участке :
01 – φ01 12 – φ12 23 –
φ23
рабочий угол поворота кулачка φраб:
φраб = φ01 + φ12 + φ23
(уб) (выс)
(сб)
Всегда независимо от схемы механизма φраб = ψраб, а
φуд ≠ ψуд,
φвыс ≠ ψвыс,
φсб ≠ ψсб,
для всех схем, кроме кулачкового механизма с центральным
толкателем.
6.3 Построение графика перемещений толкателя при заданном
профиле кулачка.
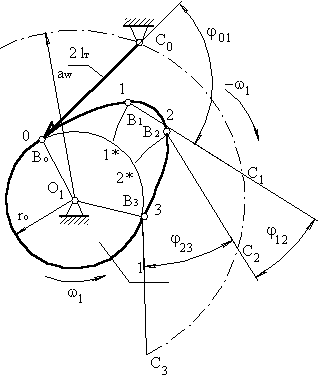
Перемещения отсчитываются от начальной окружности радиуса ro.
Точка В принадлежит толкателю, который повора - чивается вокруг оси С, т.е. т.В
перемещается по дуге окружности радиусом r = lт. Из точки 1 проводим окружность r = lт до пересечения с окружностью,
радиус которой равен расстоянию между тО1 и тС: r = aw. Точка пере сечения т.С1 – положение оси вращения толкателя в обращенном движении,
когда толкатель контактирует с поверхностью кулачка в
точке 1. Из т.С1 проводим дугу окружности r = lт до пресечения с начальной окружностью. Тогда перемещение точки В будет
равным длине дуги 11*. На участке 12 толкатель не перемещается. На участке 23 перемещение
точки В
ищется аналогично перемещению на участке 01.
|
№ |
0 |
1 |
2 |
3 |
|
|
0 |
|
|
0 |
6.4 Понятие об угле давления.
Угол давления – угол между вектором линейной скорости выходного
звена (толкателя) и реакцией, действующей с ведущего звена (кулачка) на
выходное звено. Эта реакция без учета сил трения направлена по общей нормали к
взаимодействующим поверхностям. Угол давления определяется экспериментально.
Для кулачкового механизма с поступательно движущимся толкателем допустимый угол
давления равен: [θ]
= 25Ίч35є.
Для кулачкового механизма с качающимся толкателем допустимый
угол давления равен: [θ]
= 35Ίч40є.
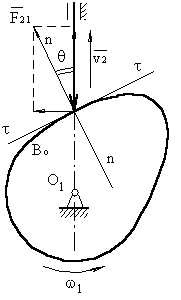
Реакцию можно разложить на две составляющие: ![]() и
и ![]() .
.
Если, в силу каких-либо причин, угол давления будет
увеличиваться, то ![]() будет уменьшаться, а
будет уменьшаться, а ![]() – увеличиваться.
– увеличиваться.
При достижении угла давления θ больше допустимого [θ],
возможен перекос оси толкателя в направляющей и его заклинивание.
6.4.1 Вывод формулы для определения
угла давления в кулачковом механизме.
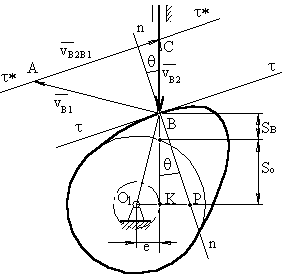
Из треугольника ΔКВР:
![]() (1)
(1)
КР = О1Р
– О1К = О1 – е
КВ = so + sB
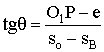 (2)
(2)
Треугольник ΔО1ВР
подобен треугольнику ΔАВС. Тогда
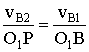 à
à 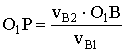
vB1=
ω1·O1B
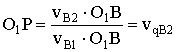
Подставим это выражение в (2):
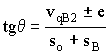
Знак “ – ” – для правой
внеосности;
знак “ + ” – для левой внеосности.
Угол давления в кулачковом механизме зависит от размеров
кулачковой шайбы: чем она больше, тем угол давления меньше.
6.4.2 Понятие об отрезке кинематических отношений.
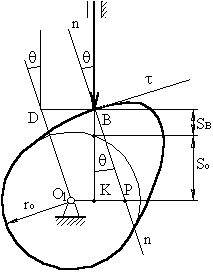
Если из точки В для какого-то текущего положения толкателя
проведем линию, параллельную О1Р, а из центра – || nn, то при их пересечении получим
точку D:
BD = O1P
= vB2 / vB1 =vqB2
Из рисунка следует, что зная перемещение точки В
толкателя и, найдя максимальный отрезок кинематического отношения, можно
определить положение центра вращения кулачка, отложив внешним образом от точки D допустимый угол давления.