Лекция 11.

5.2.2 Планетарный механизм со смешанным зацеплением

(с одним внешним и одним внутренним зацеплением).

при η= 0,99

Входное звено – первое звено;

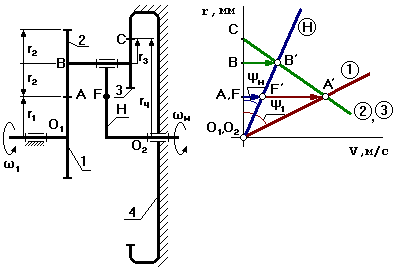
Выходное звено – водило.

1– солнечное колесо;

2,3 – блок сателлитов;

4 – коронная шестерня;

Н – водило.

Выберем на выходном звене (на водиле) точку F так, чтобы O₁A=O₂F (O₁ и O₂ соосны).

1. Графический способ определения передаточного отношения

Отрезок АА' берем произвольно.

2. Аналитический способ определения передаточного отношения.

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

1 звено: ω^*₁ = ω₁ + (–ω_н)

2 звено: ω^*₂ = ω^*₃ = ω₂ + (–ω_н)

3 звено: ω^*₃ = ω^*₂ = ω₃ + (–ω_н)

4 звено: ω^*₄ = ω₄ + (–ω_н) = –ω_н

5 звено: ω^*_н = ω_н + (–ω_н) = 0

(1)

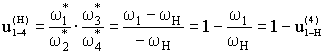
если (1) переписать через количество зубьев, то

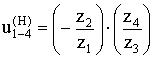
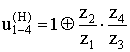
плюсовой механизм

5.2.3 Механизм с двумя внешними зацеплениями.

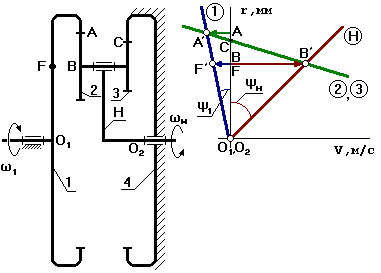
u⁽⁴⁾_1–Н = 20 ч 50 при η = 0.99

Входное звено – водило;

Выходное – первое колесо.

u⁽⁴⁾_1–Н = 1 / u⁽⁴⁾_Н–1

Например, если u⁽⁴⁾_Н–1= 20, то u⁽⁴⁾_1–Н = 1 /20

1. Графический способ.

Выберем точку F на входном звене так, чтобы O₁F = O₂B.

Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.

ψ₁ и φ₂ – направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.

2. Аналитический способ.

Применим метод обращения движения.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

Запишем передаточное отношение через число зубьев:

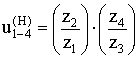
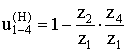
Минусовой механизм

5.2.4 Планетарный механизм с двумя внешними зацеплениями.

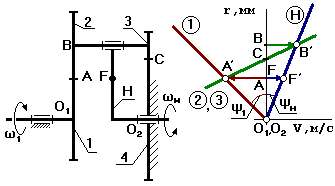
Механизм Давида

Применяется в приборных устройствах, так как u⁽⁴⁾_Н–1 до 10 000.

Недостаток – низкий К.П.Д

1. Графический способ.

Выберем на водиле Н точку F так, чтобы O₂F=O₁A (валы O₁ и O₂ соосны). Точка С может быть выше или ниже точки А.

FF' – произвольный отрезок (линейная скорость точки F).

Для колес 2 и 3 точка С – МЦС.

2. Аналитический способ.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

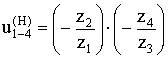
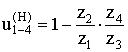
Минусовой механизм.

5.3 Синтез (проектирование) планетарных механизмов.

Под синтезом в этом курсе будем понимать подбор (определение) чисел зубьев планетарных механизмов при условии, что зубчатые колеса нулевые, а радиальный габарит механизма минимальный.

Расчет на прочность не проводим, но он обязательно должен быть проведен при проектировании.

При проектировании конструктор обязан выполнить ряд условий:

1. Отклонение от заданного передаточного отношения не должно превышать 10% (5%).

2. Обеспечить отсутствие подреза у нулевых зубчатых колес:

У колес с внешними зубьями z₁, z₂, z₃ ≥18 ;

У колес с внутренними зубьями z ≥85.

Если колеса не нулевые, то z_min от 7 для колес с внешними зубьями или z_min от 56 для колес с внутренними зубьями.

3. Обеспечить отсутствие заклинивания в зацеплении сателлит – коронная шестерня.

Заклинивания нет, если z_кш – z_сат ≥ 8

4. Обеспечить выполнение условия соосности входного и выходного звеньев.

5. Необходимо обеспечить выполнение условие соседства (окружности вершин соседних сателлитов не должны касаться друг друга).

6. Обеспечить выполнение условия сборки. Определить условие сборки, исходя из чертежа невозможно, необходимо проверить выполнение этого условия по уравнению (см. далее).

5.3.1 Проектирование однорядного планетарного механизма.

Дано:

u⁽⁴⁾_1–Н = 6

m = 1 мм

k = 3 – количество сателлитов

Определить:

z₁, z₂, z₃ – ?

при минимальном радиальном габарите;

колеса – нулевые.

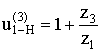à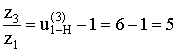

Зададимся числом зубьев z₁ так, чтобы выполнялось условие 2, тогда z₁ = 18, z₃ = 5 ^. 18 = 90 ≥ 85.

Условие соосности записывается в виде

О₁В = О₂В

r₁ + r₂ = r₃ – r₂

z₁ + z₂ = z₃ – z₂