Лекция 9.

4.5.1 Основные расчетные зависимости для определения основных параметров эвольвентных зубчатых передач.

1. Определение угла зацепления.

  (1)

где Δ_{1 ,} Δ₂ – изменение толщины зуба;

z₁ , z₂ – число зубьев.

2. Определение межосевого расстояния зубчатых передач.

+= += (2)

z_Σ = z₁ + z₂

3. Определение коэффициента воспринимаемого смещения y.

а_w = r₁ + r₂ + y m

=++ y m

(3)

4.5.2 Качественные показатели зубчатых передач.

к ним относятся:

1. Коэффициент перекрытия e a .

Характеризует плавность работы зубчатой передачи и показывает, какое число зубьев одновременно участвуют в перекрытии зацепления (насколько одна пара зубьев перекрывает работу другой).

Теоретически e a может равен 1, и это означает, что как только одна пара зубьев вышла из зацепления, следующая пара сразу же вошла в зацепление.

Если e a <1, то предыдущая пара зубьев из зацепления вышла, а следующая пара в зацепление не вошла. Такая передача работает с ударами, и ее применение недопустимо. Поэтому конструкторы при проектировании передачи считают минимально допустимым e a равным 1.05 .

Как правило, эвольвентная зубчатая передача с прямозубыми колесами имеет коэффициент перекрытия e a =1.1 – 1.5. Для косозубых колес за счет осевого перекрытия зубьев e b =e a +e g , e g 1 à e b =2.1 – 2.5

Зубчатая передача с косозубыми колесами работает более плавно, однако при этом возникает дополнительная осевая нагрузка на опоры.

2. Коэффициент удельного давления n .

Характеризует прочностные характеристики передачи с точки зрения контактных напряжений в высшей КП.

3. Коэффициент удельного скольжения l .

Характеризует износостойкость зубчатой передачи в высшей КП.

4.5.3 Определение коэффициента перекрытия графическим способом.

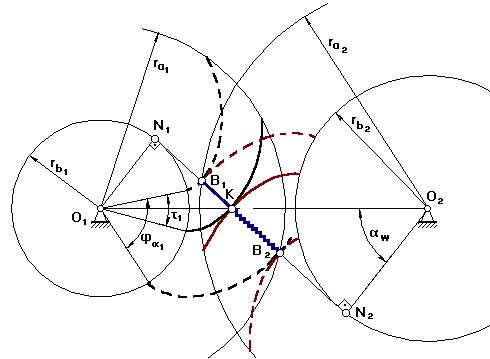
B₁B₂ рабочий участок линии зацепления N₁N₂.

В точке В₁ пара эвольвент входит в зацепление. При повороте на угол x_a эта пара эвольвент касается в т. К, а в т.В₁ в зацепление вошла следующая пара эвольвент, и участок КВ₂ обе пары эвольвент проходят вместе, т.е. вторая пара эвольвент перекрывает работу первой пары. Тогда e a равен

e a = ,

где j a ₁ – угол перекрытия первого колеса.

j a ₁ = r_b1

e a =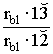

Т.к. линия зацепления перекатывается по основной окружности без скольжения, то

= B₁B₂ , =B₁K

e a =

4.6 Способы изготовления зубчатых колес

Существуют два основных способа изготовления зубчатых колес:

1. копирование: профиль зуба инструмента (протяжка) переносится на заготовку. Способ очень неточный, малопроизводительный и требует наличие инструмента в большом ассортименте, различаемых по модулю и количеству зубьев. Применяется в мелко серийном производстве.

2. огибание (см. лаб.раб. №8): инструменту и заготовке сообщают такое относительное движение, при котором огибающая к положению режущей кромке инструмента очерчивает эвольвенту. Инструмент может быть различным: рейки (гребенки), долбяки и фрезы.

4.6.1 Понятие о производящем исходном контуре реечного инструмента.

Производящий исходный контур – проекция режущей грани инструмента на плоскость, перпендикулярную оси вращения заготовки.

Рейка – зубчатое колесо с теоретически бесконечно большим количеством зубьев. Как привило, их бывает 8.

r_b à , поэтому все окружности и эвольвента – прямые.

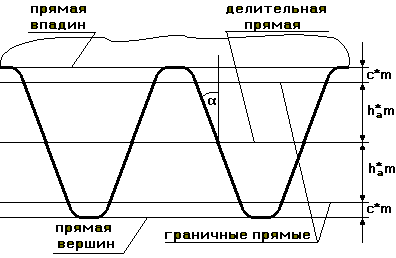
Все параметры по делительной прямой и по прямым, параллельным делительной прямой, стандартизированы.

a =20^о ; h_a* - коэффициент высоты зуба (по ГОСТ h_a*=1).

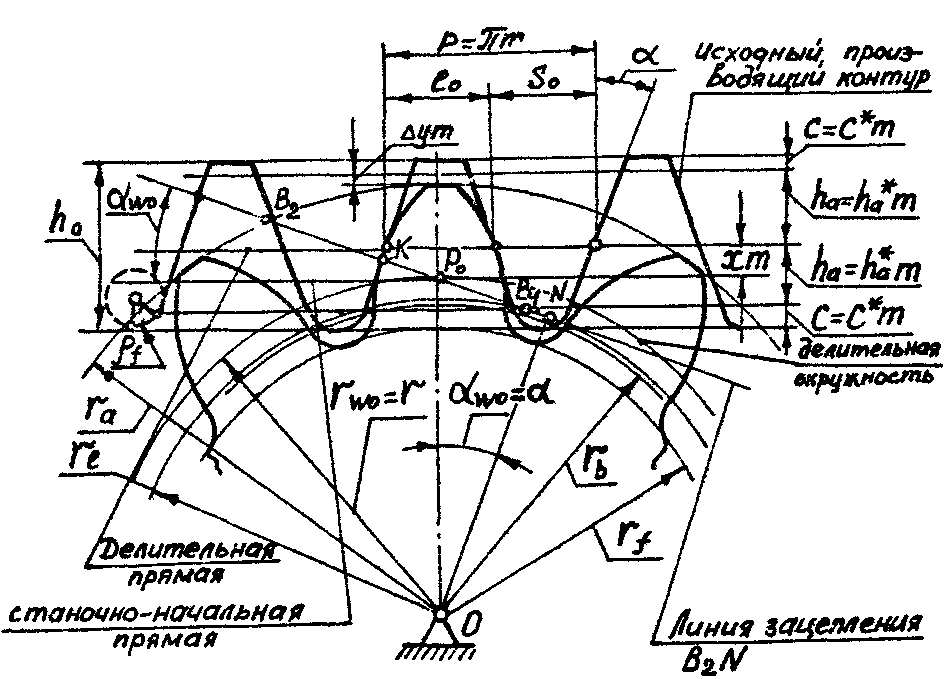
4.6.2 Станочное зацепление.

Станочное зацепление – зацепление заготовки и инструмента (см. рис. 10-86).

Xm -	смещение исходного производящего контура;
Δym -	уравнительное смещение;
P0 -	полюс зацепления;
α W0=α -	угол зацепления в станочном зацеплении;
rW0 = r = mz/2 -	радиус начальной окружности, равный радиусу делительной окружности;
B1B2 < B2N -	длина активной линии зацепления;
Ri=OB1 -	радиус окружности граничных точек

Рис.10-86. Схема станочного зацепления

Параметры, относящиеся к инструменту, имеют индекс ‘_o’

e_o – ширина впадины инструмента по делительной прямой,

s_о – толщина зуба инструмента по делительной прямой.

У инструмента всегда e_o = s_o, r_wo = r.

В станочном зацеплении начальная окружность всегда совпадает с делительной окружностью, т.к. необходимо перенести с инструмента стандартные параметры: шаг р, модуль m и угол профиля a . Эти стандартные параметры имеют место на делительной окружности или на прямой, параллельной делительной прямой.

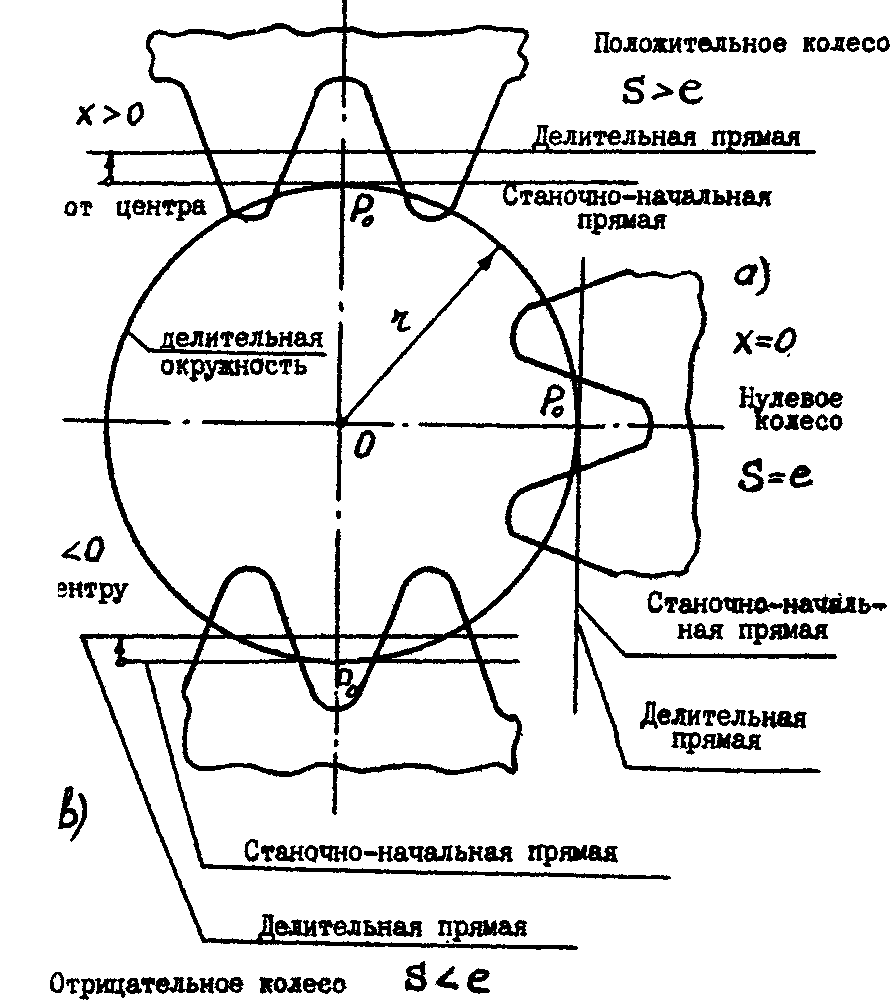
По отношению к делительной окружности заготовки, делительная прямая может занимать следующие положения (рис. 17-89):

Рис.I7-89. Схема” определяющая знак колеса

1. инструмент отодвигается от центра заготовки и между делительной окружностью заготовки и делительной прямой инструмента имеет место смещение х^.m, где х – коэффициент смещения инструмента, который имеет знак.

В рассматриваемом случае x>0, xm>0 – нарезается положительное зубчатое колесо.

Прямая инструмента, касательная к делительной окружности заготовки – станочно-начальная прямая.

2. делительная прямая инструмента является станочно-начальной прямой, т.е. касается делительной окружности. х=0, хm=0 – нулевое зубчатое колесо.

3. при смещении инструмента к центру заготовки, между делительной прямой и делительной окружностью смещение xm<0, x<0 – отрицательное зубчатое колесо.

Коэффициент изменения толщины зуба Δ:

Δ=2^.x^.tga

Вопрос: в каком диапазоне может перемещаться инструмент?

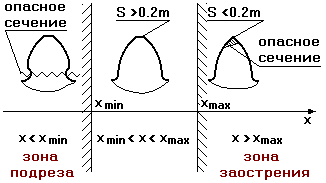
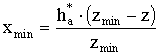
где x_min – минимальный коэффициент смещения инструмента, при котором наступает подрез зуба.

Если В₁ выйдет за N, то будет подрез ( В₁ – точка пересечения граничной прямой рейки с линией зацепления, а N – точка касания линии зацепления с основной окружностью).