Лекция 5.
Для
определения угловой скорости
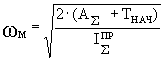,где 
const var
Для
того чтобы удерживать колебания угловой скорости w м
в заданных пределах, определяемых коэффициентом неравномерности d , первая
группа звеньев должна иметь 
2.6.3 Вывод формулы для определения .
Изменение
w м от w м_max до w м_min приводит к изменению
кинетической энергии первой группы звеньев (ΔТI), которое равно:
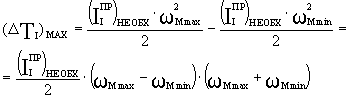
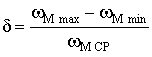
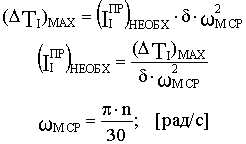(2)
При
установившемся режиме работы при определении w м формулу (1) напрямую использовать нельзя, т.к.
неизвестно Тнач, поэтому задачу решают,
используя метод Мерцалова
(см. учебник).
2.7 Определение реакций в кинематических парах
рычажных механизмов без учета трения.
Данная
задача может быть решена:
1. аналитическим способом;
2. графическим способом (см.ДЗ №2).
Аналитический способ:
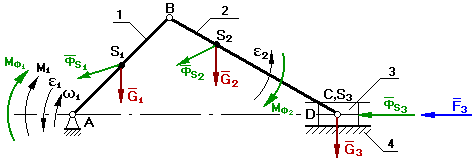
Изобразим
схему кривошипно-ползунного механизма.
Дано:
F3,
G1, ФS1, MФ1, G2,
ФS2, МФ2, G3, ФS3,
w i, e i, vi, ai.
Определить:
М1 и Qij
Задачу
начинают решать с того звена, к которому приложена известная сила или момент.
Кроме того, введем понятие входной
шарнир (проекции реакции Q на оси х и у положительны) и выходной шарнир (проекции реакции Q на оси -
отрицательны).
Расстояние
от входного шарнира до центра масс звена – р, а расстояние от выходного шарнира до центра масс
звена – q.
Звено 1
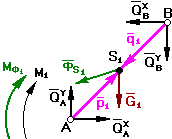
Шарнир А - входной
Шарнир В - выходной
Звено 2
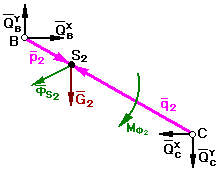
Шарнир В - входной
Шарнир С - выходной
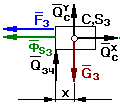Звено
3
При
решении задачи используется принцип Даламбера
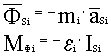
3
звено:
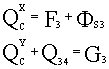
2
звено:
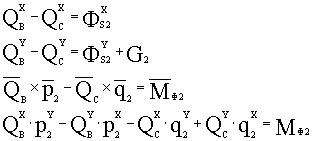
1
звено:
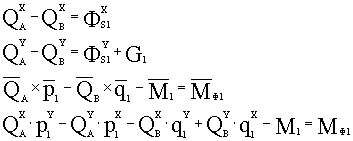
Составим
систему уравнений в матричной форме:
|
неизвестные |
QAx |
QAy |
QBx |
QBy |
QCx |
QCy |
Q34 |
M1 |
||||||
|
F3+ФS3 |
= |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
х |
QAx |
|||
|
G3 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
QAy |
|||||
|
ФS2x |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
QBx |
|||||
|
ФS2y+G2 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
QBy |
|||||
|
MФ2 |
0 |
0 |
p2y |
-p2x |
-q2y |
q2x |
0 |
0 |
QCx |
|||||
|
ФS1x |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
QCy |
|||||
|
ФS2y+G2 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
Q34 |
|||||
|
MФ1 |
p1y |
-p1x |
-q1y |
q1x |
0 |
0 |
0 |
-1 |
M1 |
|||||
b
= A·x
Эта
система решается методом Гаусса.
2.8 Учет трения при определении реакций в
кинематических парах.
Трение является сложным
физико-химическим процессом, сопровождающийся
выделением тепла. Это вызвано тем, что перемещающиеся тела оказывают
сопротивление относительному движению. Мерой интенсивности сопротивления
относительному перемещению является сила (момент) трения.
Различают
трение качения, трение скольжения, а также сухое, граничное и жидкостное
трение.
Если
суммарная высота микронеровностей взаимодействующих поверхностей:
- больше, чем
высота слоя смазки, то - сухое
трение.
- равна высоте слоя смазки, то - граничное трение.
- меньше, чем
высота слоя смазки, то - жидкостное .
1. Учет трения в поступательной кинематической паре.
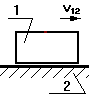Без
учета трения реакция направлена по нормали к взаимодействующим поверхностям.
При учете трения результирующая реакция Q21 отклоняется от общей
нормали на угол трения j в
сторону противоположную направлению движения.
без учета трения с учетом трения
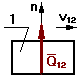
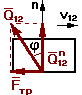Fтр=Qn12.tg j
tg j = f
Fтр=Qn12.f
Коэффициент трения f определяется экспериментально и зависит от многих
факторов.
2. Учет трения во вращательной кинематической паре.
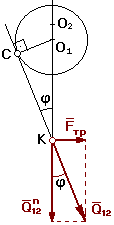
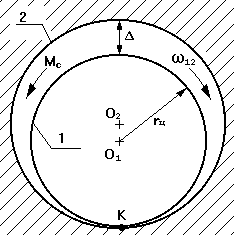
1 -
цапфа
rц - радиус
цапфы
Δ -
зазор
r - радус круга трения;
r = О1С
Из ΔО1СК
à 
= sin j à О1С = О1К sin
j
Mc= Q12.О1С = Q12.
rц.sin
j
При
малых углах j sin j ≈ tg j = f . Тогда
:
Mc= Q12. rц.f
При учете трения во вращательной КП результирующая
реакция отклоняется от общей нормали на угол трения j и проходит касательно к кругу трения
радиуса r