Лекция 3.

Продифференцируем (3) по обобщенной координате:

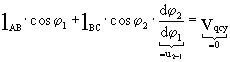
(5)

Продифференцируем (2) по обобщенной координате:

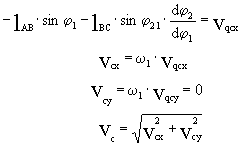
Если необходимо определить функции положения центра масс, то рассматривается векторный контур

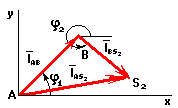
Условие замкнутости данного векторного контура имеет вид:

(6) Спроецируем данный векторный контур на оси координат

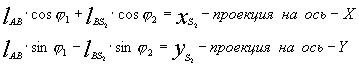(7)

Продифференцируем (7) по обобщенной координате и получим аналоги линейных скоростей точек S₂ в проекциях на оси х и у:

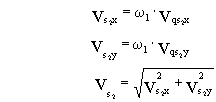(9)

2. Анализ машинного агрегата.

В данной главе будут рассмотрены следующие вопросы:

1. Силы и моменты, действующие в машинном агрегате.

2. Переход от расчетных схем машинных агрегатов к динамическим моделям.

3. Расчет усилий в кинематических парах основного механизма рабочей машины.

4. Определение законов движения главного вала (входного звена) рабочей машины под действием приложенных сил и моментов при различных режимах работы машинного агрегата.

2.1 Силы и моменты, действующие в машинном агрегате.

2.1.1 Движущиеся силы и моменты F_д и М_д.

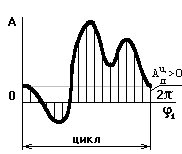
Работа движущих сил и моментов за цикл положительна: А_д>0.

Цикл – промежуток времени, по истечению которого все кинематические параметры принимают первоначальное значение, а технологический процесс, происходящий в рабочей машине, начинает повторяться .

2.1.2 Силы и моменты сопротивления F_с,M_с.

Работа сил и моментов сопротивления за цикл отрицательна: А_c<0.

2.1.3 Силы тяжести (G_i).

Работа силы тяжести за цикл равна нулю: А_Gi=0.

2.1.4 Расчетные силы и моменты Ф_Si,M_Фi.

Ф_Si,M_Фi – Главные векторы сил инерции и главные моменты от сил инерции.

2.1.5 Реакции в кинематических парах Q_ij.

2.2 Понятие о механических характеристиках. Каждая рабочая машина имеет свою механическую характеристику, которая приводится в техническом паспорте машины. Примеры механических характеристик некоторых машин приведены ниже.

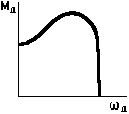
Механическая характеристика 3-х фазного асинхронного двигателя.

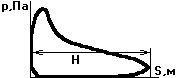
Индикаторная диаграмма ДВС

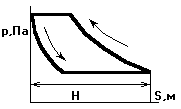
H – ход поршня в поршневой машине

(расстояние между крайними

положениями поршня)

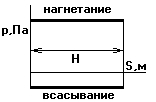
Индикаторная диаграмма насоса

Как правило, из паспорта известен диаметр поршня, по нему можно определить площадь S_п= p ^.d²/4, тогда сила: F=p^.S_п

Правило знаков сил и моментов:

• Сила считается положительной, если она по направлению совпадает с направлением движения того звена, к которому эта сила приложена.
• Момент считается положительным, если его направление совпадает с направлением угловой скорости вращения данного звена.

Имея механическую характеристику поршневой машины в виде индикаторной диаграммы и учитывая правило знаков, можно перестроить её в график сил (см. лабораторную работу №4).

Основной вывод:

В течение всего цикла работы поршневой машины сила, приложенная к поршню, будет изменяться как по величине, так и по направлению, это в свою очередь приводит к колебаниям угловой скорости главного вала рабочей машины.

2.3 Понятие о расчетной схеме машинного агрегата и переход от нее к динамической модели.

На расчетной схеме машинного агрегата отмечают основные силовые факторы, действующие в машинном агрегате; основные массы звеньев, влияющих на закон движения машинного агрегата; и основные жесткости валов. На рис.5-92 показан переход от реальной схемы к расчетной схеме (а) и от нее к динамической модели.

Из множества масс выделены 3 основные, оказывающие самое большое влияние на закон движения.

Расчетная схема (б) – 3-х массовая динамическая модель.

Для описания закона движения 3-х массовой динамической модели необходимо 3 дифференциальных уравнения.

Если положить жесткость с₁ , то можно перейти к двумассовой модели (необходимо 2 диф. уравнения).

Если положить жесткость с₂ , то получим одномассовую динамическую модель (рис. 2.3).

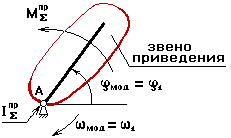
Рис. 2.3

Можно иметь 2 вида одномассовых динамических моделей:

1. Если звено приведения совершает вращательное движение, то одномассовая модель имеет вид

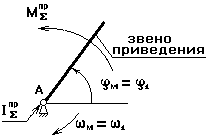
закон движения должен быть один,

поэтому w _м = w ₁ , j _м = j ₁

Уравнение движения можно записать одним уравнением, в виде изменения кинетической энергии:

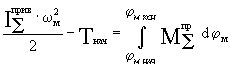
2. 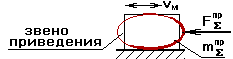Если звено приведения совершает поступательное движение, то одномассовая модель имеет вид:

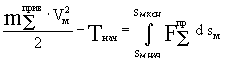
Этот вид модели за недостатком времени рассматривать не будем.

2.4 Приведение сил и масс к одномассовой динамической модели.

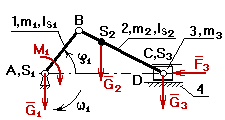
j ₁ – обобщенная координата.

Нужно определить закон движения 1-го

звена данного механизма.

Дано: j ₁, w ₁, l_AB, l_BC, l_BS2, G₂, G₃, F₃, I_S1, I_S2.

Определить, как изменяется w ₁.

При переходе от расчетной схемы к одномассовой динамической модели за звено приведения, как правило, принимают то звено, закон движения которого определяют.

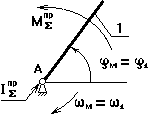
Звено приведения – зв.1; оно совершает вращательное движение, следовательно, одномассовая динамическая модель имеет вид:

2.4.1 Приведение масс.

При переходе от расчетной схемы к модели необходимо обеспечить равенство кинетической энергии звена динамической модели и суммы кинетических энергий реальных звеньев механизма:

Т_Мод = Т_Мех .

Кинетическая энергия модели должна быть равна кинетической энергии всего механизма.

Т_мод = Т_пост + Т_вращ

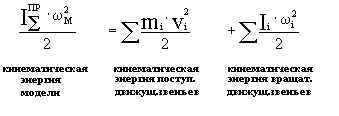
В нашем случае:

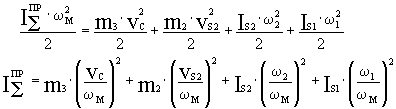
w _м = w ₁